BBvsBTN(3betpot)におけるCB戦略について(理論値)
24時過ぎに投稿するよりは19時頃の方が目に留まりやすいかなと思い、前回、予約投稿機能と予約投稿ツイート機能を使ったところ、なんかツイートが変な感じになってしまったようです。
でも、これがあれば複数回分の記事を書き溜めて自動でポンポン放出できて良いですね。
記事を書き始めるとつい自分で盛り上がって突っ走ってしまう結果、1記事が長すぎる気もするので、意識して小分け投稿勢にシフトしたいもんです。
●BBvsBTN(3betpot)におけるベンチマーク・「理論値」の導出
まず前提として、GTO戦略は、複数のBetおよびアクションをかなり複雑に混合しており、実践でそうそう真似できるものではありません。
例として、下図は前回のシチュエーション(BBvsBTN(3betpot))での[Kd8d4h]におけるBBのCB戦略(GTO(Check/Bet(25%pot)/Bet(36%)/Bet(50%)/Bet(70%)/Bet(100%)))です。
ハンドごとの色分けを見ると、それぞれのハンドについて、BBのアクション比率がかなり細かく設定されていることがわかります。
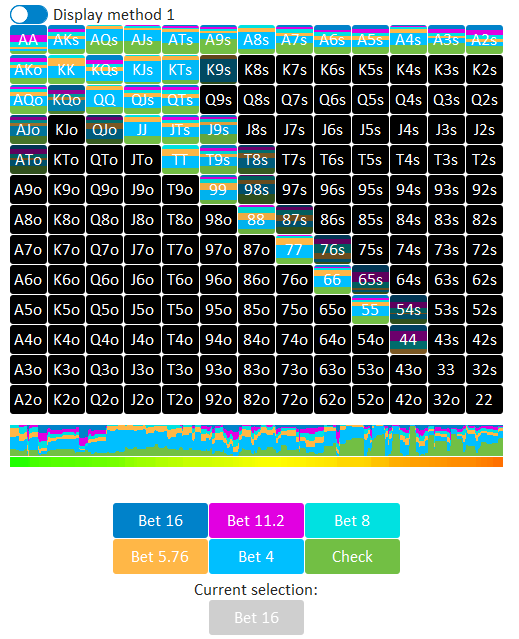
しかし、GTOの最適アクション比率は混合されすぎているため、これを実戦で真似しようとするのは、かなり骨が折れそうです。
むしろ、アクションごとの最適頻度を気にしなければ、どのアクションをしてもGTO的に正解になるんじゃないかとすら思えます。
そこで、こうした混合戦略について、実践で活用できるよう簡単な「疑似GTO戦略」を体系化することがひとまずの目的です。
そのために、前回のシチュエーションをもとに、BBのCB戦略の理論値を考察します。
(ここでいう「理論値」とは、BBが複数のBetサイズを混合したGTOに基づき、特定のストリートで最適にアクションを採った場合に得られるEVとします。
EVは、以降のストリートでプレイヤーが最適にアクションした場合の期待値です。)
そして、理論値として計算されたEVと「疑似GTO戦略」によるEVの差が小さければ、「疑似GTO戦略」を最適GTO戦略の代替として活用することができそうです。
●CB戦略による理論値の導出
ということで、1000フロップにおける理論値を導出します。
ちなみに、ポジションの優位性云々は置いといて、OOPの分析はIPより簡単です。
というのも、先般のBTNvsBB(2bet pot)と異なり、OOPの分析の特徴として、主に以下のことがあります。
・IPと異なり、Check or Betによってストリートの分岐が変わらない
(IPの分析では、自分のCheckによってターンに進むが、Betによって相手の「Fold or Call or Raise」アクションに進む。)
⇒OOPの分析では、「Check=Bet 0%pot」とみなし、HeroによるCBの平均Betサイズを比較的簡単に計算することができる。
・相手のdonk Betを考慮せずにすむ
⇒BBは、「Preflop3bet→FlopCB戦略」の一連の流れを確実に実行できる。
そんなOOP分析について、今回のBBvsBTN(3betpot)における理論値が以下の図になります。
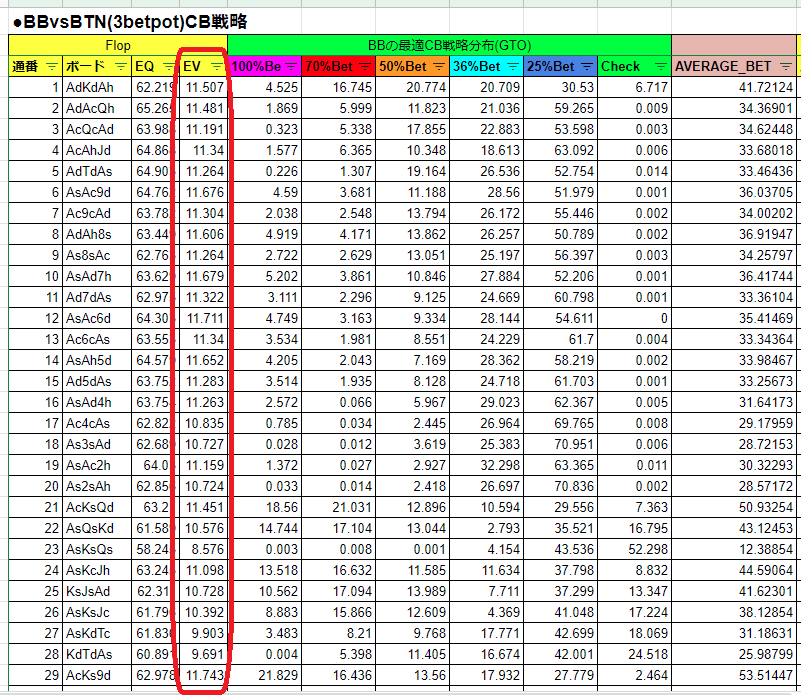
通番が1~29しか映っていませんが、こんな調子で下には1000番まであります。
GTO+の良いところは、最近のアップデートでフロップボードのハイカード順にソートを並び替えてくれるところです。
ここでのGTO戦略は、前掲のとおり、GTO(Check/Bet(25%pot)/Bet(36%)/Bet(50%)/Bet(70%)/Bet(100%)の6種類のアクションを選択肢とし、これによって得られるEV値を今後の分析における「理論値」とします。
(本当は、Betサイズを1%区切りで200種類くらいのアクションをGTOに入れれば、より精緻な「理論値」が導出されますが、あまりに時間がかかるので省略します。)
ボードごとのEQ(エクイティ)は、GTOの結果云々に関わらず、ハンドレンジvsハンドレンジによって導出されるので、どんなCB戦略を採ろうと一定です。
私たちが追い求めるべき数値は、CB戦略の変化によってもたらされる赤枠内「EV」にあります。
では、1~1000番におけるEV値およびBetサイズの平均理論値は、どんな値でしょう?
1~1000番のボードについて、平均値を導出しました。

この図から、1,000ボードの16.00bbのpotに対し、BBが最適CB戦略を採った場合の平均理論値は、9.09bbとなりました。
また、BBの平均Betサイズは、右のAVERAGE_BETのとおり、33.18%potでした。
16.00bbのpotに対して9.09bbというと、BBは適切にCBを打てば、フロップ時点で平均56.8%のpotがEVとして見込めることになります。
この「56.8%」というのも、なんだか多いような少ないような数値ですね。
ですが、とりあえず3bet側はちゃんとした戦略でCBを打っていれば、potの55%を超えるEVを得られることがわかりました。
言い換えると、BBがプリフロ→フロップにかけて適切なハンドレンジおよびCB戦略を備えていれば、3betpotを開くたび、BBは平均1.25bb程度の利益(9.09bb-7.75bb:「flopのEV」-「Preflopの3bet額」)を獲得できるともいえそうです。
(3betによる相手のFoldやvs4bet等の展開を加味しない単純計算です。)
以上、今後の分析でベンチマークとして用いる理論値を計算できました。
次回は参考として、この理論値をボードのファクターごとに分析してみます。